已知二次函数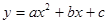 的图象经过点(-2,4),(-1,0),(0,-2)
的图象经过点(-2,4),(-1,0),(0,-2)
(1)求这个二次函数的表达式
(2)求此二次函数的顶点坐标及与坐标轴的交点坐标,并根据这些点画出函数大致图象
(3)若0<y<3,求x的取值范围
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC、CD上,若△ADE∽△CMN,求CM的长.
如图,在等腰梯形ABCD中,∠B=60°,且AB=AD=CD,请你将等腰梯形分成3个三角形,使得其中有两个是相似三角形,且相似比不为1.
现在请你参考示意图,另外再给出三种分割方法(注:在两个相似三角形中标明必要的角度.)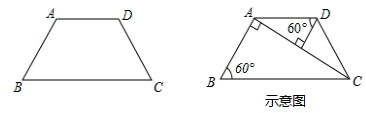


△ABC∽△A′B′C′, ,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求:
,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求:
(1)A′B′边上的中线C′D′的长;
(2)△A′B′C′的周长;
(3)△ABC的面积.
如图,已知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于多少?(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于多少?(结果保留根号).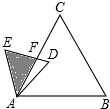
已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k.
(1)如果CD和C′D′是它们的对应高,那么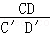 等于多少?
等于多少?
(2)如果CD和C′D′是它们的对应角平分线,那么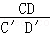 等于多少?如果CD和C′D′是它们的对应中线呢?
等于多少?如果CD和C′D′是它们的对应中线呢?