某校从6名教师中,选派4名同时到3个边远地区支教,每个地区至少选派1名.
(Ⅰ) 共有多少种不同的选派方法?
(Ⅱ) 若6名教师中的甲,乙二位教师不能同时支教,共有多少种不同的选派方法?
(本小题满分13分)已知数列 是等差数列,
是等差数列, 为其前n项和,
为其前n项和, .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和.
的前n项和.
(本小题满分13分)设函数 的定义域为A,集合
的定义域为A,集合 .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若集合 中恰有一个整数,求实数a的取值范围.
中恰有一个整数,求实数a的取值范围.
(本小题满分14分)已知函数 ,
,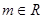 ,令
,令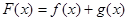 .
.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式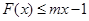 恒成立,求整数m的最小值;
恒成立,求整数m的最小值;
(Ⅲ)若 ,且正实数
,且正实数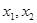 满足
满足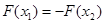 ,求证:
,求证: .
.
(本小题满分14分)已知函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点(0,1)处的切线方程;
在点(0,1)处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为0,求a的值;
上的最小值为0,求a的值;
(Ⅲ)若对于任意 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(本小题满分13分)盒中装有7个零件,其中5个是没有使用过的,2个是使用过的.
(Ⅰ)从盒中每次随机抽取1个零件,有放回的抽取3次,求3次抽取中恰有2次抽到使用过零件的概率;
(Ⅱ)从盒中任意抽取3个零件,使用后放回盒子中,设X为盒子中使用过零件的个数,求X的分布列和期望.