(本小题满分14分)已知函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点(0,1)处的切线方程;
在点(0,1)处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为0,求a的值;
上的最小值为0,求a的值;
(Ⅲ)若对于任意 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知函数 .
.
(Ⅰ) 若 ,求函数
,求函数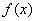 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的斜率是1,问:
处的切线的斜率是1,问: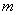 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的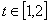 ,函数
,函数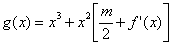 在区间
在区间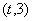 上总存在极值?
上总存在极值?
已知数列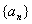 满足
满足 ,
,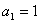 .
.
(Ⅰ) 求数列{ 的前
的前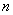 项和
项和 ;
;
(Ⅱ)若存在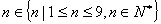 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,在四棱锥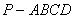 中,底面
中,底面 是边长为2的正方形,且
是边长为2的正方形,且 ,
,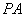 =
=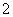 ,
, 为
为 的中点. 求:
的中点. 求:
(Ⅰ) 异面直线CM与PD所成的角的余弦值;
(Ⅱ)直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.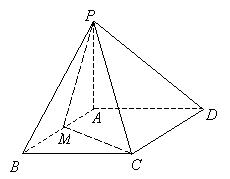
已知数列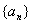 是公差大于
是公差大于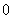 的等差数列,且满足
的等差数列,且满足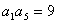 ,
, .
.
(Ⅰ) 求数列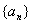 的通项公式;
的通项公式;
(Ⅱ)若数列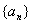 和数列
和数列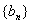 满足等式
满足等式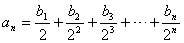 (
( ),求数列
),求数列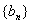 的前
的前 项和
项和 .
.
某学校拟建一块周长为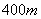 的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到
的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到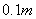 ,取
,取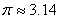 )
)
