学校为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和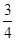 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响.
(Ⅰ)求移栽的4株大树中恰有3株成活的概率;
(Ⅱ)设移栽的4株大树中成活的株数为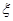 ,求
,求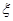 分布列与期望.
分布列与期望.
(本小题满分12分)已知函数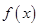 =" |" x +1|−|2x−1|。
=" |" x +1|−|2x−1|。
(1)求不等式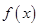 ≥0的解集;
≥0的解集;
(2)若不等式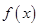 <a对任意x∈R恒成立,求实数a的取值范围。
<a对任意x∈R恒成立,求实数a的取值范围。
已知函数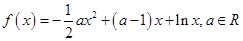 .
.
(1)讨论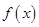 的单调性;
的单调性;
(2)证明:当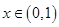 时,
时,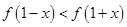 ;
;
(3)若函数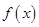 有两个零点
有两个零点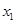 ,
,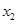 ,比较
,比较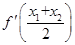 与
与 的大小,并证明你的结论。
的大小,并证明你的结论。
如图,已知抛物线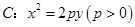 ,其焦点
,其焦点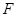 到准线的距离为
到准线的距离为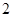 ,点
,点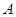 、点
、点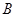 是抛物线
是抛物线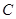 上的定点,它们到焦点
上的定点,它们到焦点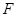 的距离均为
的距离均为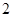 ,且点
,且点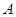 位于第一象限.
位于第一象限.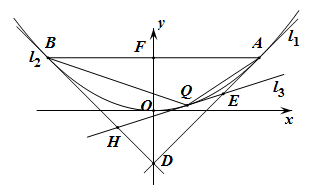
(1)求抛物线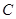 的方程及点
的方程及点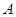 、点
、点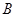 的坐标;
的坐标;
(2)若点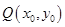 是抛物线
是抛物线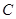 异于
异于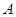 、
、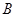 的一动点,分别以点
的一动点,分别以点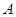 、
、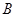 、
、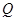 为切点作抛物线
为切点作抛物线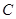 的三条切线
的三条切线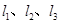 ,若
,若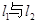 、
、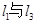 、
、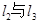 分别相交于D、E、H,设
分别相交于D、E、H,设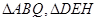 的面积依次为
的面积依次为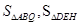 ,记
,记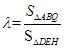 ,问:
,问: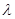 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标为  ,当
,当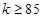 时,产品为一级品;当
时,产品为一级品;当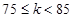 时,产品为二级品;当
时,产品为二级品;当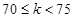 时,产品为三级品。现用两种新配方(分别称为A配方和B配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(以下均视频率为概率)
时,产品为三级品。现用两种新配方(分别称为A配方和B配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(以下均视频率为概率)

(1)若从B配方产品中有放回地随机抽取3件,记“抽出的B配方产品中至少1件二级品”为事件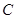 ,求事件
,求事件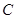 的概率
的概率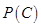 ;
;
(2)若两种新产品的利润率 与质量指标值
与质量指标值 满足如下关系:
满足如下关系: ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?
已知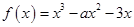 ,其中
,其中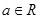 .
.
(1)当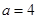 时,求
时,求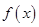 在[-1,1]上的最大值;
在[-1,1]上的最大值;
(2)若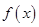 在
在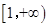 上存在单调递减区间,求
上存在单调递减区间,求 的取值范围。
的取值范围。