随机抽取某厂的某种产品100件，经质检，其中有一等品63件、二等品25件、三等品10件、次品2件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为
．
（1）求的分布列；
（2）求1件产品的平均利润（即的数学期望）；
（3）经技术革新后，仍有四个等级的产品，但次品率降为
，一等品率提高为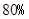
．如果此时要求1件产品的平均利润不小于5.13万元，则三等品率最多是多少？
如图，在四棱锥P—ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB＝4，PA＝3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC.
（1）求证：AG∥平面PEC；
（2）求AE的长；
（3）求二面角E—PC—A的正弦值.
甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为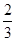
，乙能攻克的概率为
，丙能攻克的概率为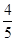
.
（1）求这一技术难题被攻克的概率；
（2）若该技术难题末被攻克，上级不做任何奖励；若该技术难题被攻克，上级会奖励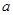
万元。奖励规则如下：若只有1人攻克，则此人获得全部奖金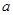万元；若只有2人攻克，则奖金奖给此二人，每人各得
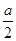万元；若三人均攻克，则奖金奖给此三人，每人各得
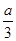万元。设甲得到的奖金数为X，求X的分布列和数学期望。
在△ABC中，内角A，B，C所对边长分别为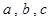
，
，
， 
.
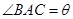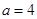（1）求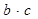
的最大值及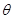
的取值范围；
（2）求函数
的最值.
（本小题满分14分）
已知
（Ⅰ）求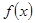
；
（Ⅱ）判断并证明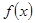的奇偶性与单调性;
（Ⅲ）若对任意的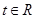
，不等式
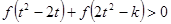恒成立，求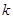
的取值范围。
（本小题满分12分）为了预防流感，某学校对教室用药熏消毒法进行消毒.已知药物释放过程中，室内每立方米空气的含药量
（毫克）与时间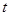
（小时）成正比.药物释放完毕后，与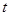的函数关系式为
（
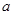为常数），如图所示，根据图中提供的信息，回答下列问题：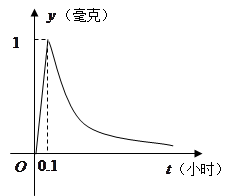
（1）求从药物释放开始，每立方米空气中的含药量（毫克）与时间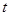（小时）之间的函数关系式；（2）据测定，当空气中每立方米空气的含药量降到0．25毫克以下时，学生方可进教室，那从药物释放开始，至少需要经过多少小时后，学生才能回到进教室？