(本小题满分13分)
已知函数 ,其中
,其中 是常数.
是常数.
(Ⅰ)当 时,求
时,求 曲线
曲线 在点
在点
 处的切线方程;
处的切线方程;
(Ⅱ)若存在实数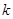 ,使得关于
,使得关于 的方程
的方程 在
在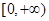 上有两个不相等的实数根,求
上有两个不相等的实数根,求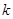 的取值范围.
的取值范围.
已知函数f(x)=()x,
函数y=f-1(x)是函数y=f(x)的反函数.
(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a);
(3)是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由
设函数f(x)=x2+x-.
(1)若函数的定义域为[0,3],求f(x)的值域;
(2)若定义域为[a,a+1]时,f(x)的值域是[-,],求a的值
某工厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价恰为51元;
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少?如果订购1 000个,利润又是多少?(工厂售出一个零件的利润=实际出厂单价-成本
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性.
已知函数f(x)=-xm,且f(4)=-.
(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明