现有8名数理化成绩优秀者,其中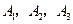 数学成绩优秀,
数学成绩优秀,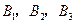 物理成绩优秀,
物理成绩优秀,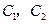 化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛
化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛
(Ⅰ)求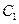 被选中的概率;
被选中的概率;
(Ⅱ)求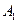 和
和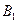 不全被选中的概率
不全被选中的概率
已知圆C过定点A(0,p)(p>0),圆心C在抛物线x2=2py上运动,若MN为圆C在x轴上截得的弦,设|AM|=m,|AN|=n,∠MAN=θ.
(1)当点C运动时,|MN|是否变化?写出并证明你的结论?
(2)求 +
+ 的最大值,并求取得最大值时θ的值和此时圆C的方程.若不存在,说明理由
的最大值,并求取得最大值时θ的值和此时圆C的方程.若不存在,说明理由
△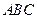 中,内角
中,内角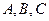 的对边分别为
的对边分别为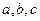 ,已知
,已知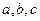 成等比数列,
成等比数列,
求(1) 的值;(2)设
的值;(2)设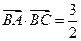 ,求
,求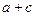 的值.
的值.
抛物线x2=4y的焦点为F,过点(0,-1)作直线l交抛物线A、B两点,再以AF、BF为邻边作平行四边形FABR,试求动点R的轨迹方程.
已知抛物线y2=4ax(0<a<1)的焦点为F,以A(a+4,0)为圆心,|AF|为半径在x轴上方作半圆交抛物线于不同的两点M和N,设P为线段MN的中点,
(Ⅰ)求|MF|+|NF|的值;
(Ⅱ)是否存在这样的a值,使|MF|、|PF|、|NF|成等差数列?如存在,求出a的值,
已知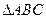 中,
中, ,则
,则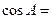
A.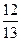 |
B.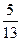 |
C. |
D.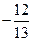 |