已知,数列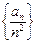
 是公比为
是公比为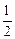 的等比数列,
的等比数列,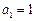 .
.
(1)求数列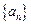 的通项公式;
的通项公式;
(2)令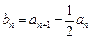 ,若数列
,若数列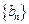 的前
的前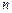 项和
项和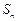 ,求证:
,求证: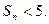
如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm).(加工中不计损失).

(1)若钉身长度是钉帽高度的2倍,求铆钉的表面积;
(2)若每块钢板的厚度为 mm,求钉身的长度(结果精确到
mm,求钉身的长度(结果精确到 mm).
mm).
已知函数 满足
满足
(1)求实数 的值以及函数
的值以及函数 的最小正周期;
的最小正周期;
(2)记 ,若函数
,若函数 是偶函数,求实数
是偶函数,求实数 的值.
的值.
已知 是椭圆
是椭圆 上的一点,求
上的一点,求 到
到 (
( )的距离的最小值.
)的距离的最小值.
若在边长为 的正三角形
的正三角形 的边
的边 上有
上有 (
( N*,
N*, )等分点,沿向量
)等分点,沿向量 的方向依次为
的方向依次为 ,记
,记 ,若给出四个数值:①
,若给出四个数值:① ②
② ③
③ ④
④ ,则
,则 的值不可能的共有()
的值不可能的共有()
| A.1个 | B.2个 | C.3个 | D.4个 |
已知数列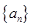 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若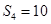 ,
,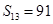 .
.
(1)求 ;
;
(2)若数列{Mn}满足条件: 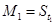 ,当
,当 时,
时,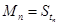 -
-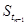 ,其中数列
,其中数列 单调递增,且
单调递增,且 ,
, .
.
①试找出一组 ,
,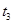 ,使得
,使得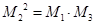 ;
;
②证明:对于数列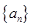 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列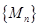 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.