(本小题满分12分)
某工厂为了对新研发的一种产品进行合理定价,将对该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
| 销售y(件) |
90 |
84 |
83 |
80 |
75 |
68 |
(1)请根据上表提供的数据,用最小二乘法求出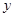 关于
关于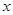 的线性回归方程
的线性回归方程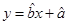 ;
;
其中(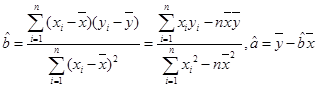 )
)
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
(本题满分16分,第(1)小题7分,第(2)小题9分)
如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等.铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm,加工中不计损失).
(1)若钉身长度是钉帽高度的2倍,求铆钉的表面积;
(2)若每块钢板的厚度为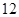 mm,求钉身的长度(结果精确到
mm,求钉身的长度(结果精确到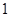 mm).
mm).
(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,在四棱锥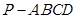 中,底面
中,底面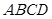 为矩形,
为矩形, 平面
平面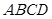 ,点
,点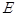 在线段
在线段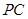 上,
上,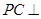 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的大小.
的大小.
(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,已知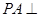 平面
平面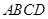 ,
, ,
,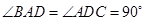 .
.
(1)求直线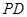 与平面
与平面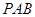 所成角的大小;
所成角的大小;
(2)求点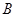 到平面
到平面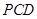 的距离.
的距离.
(本题满分12分,第(1)小题4分,第(2)小题8分)
如图,在体积为16的正四棱柱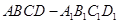 中,点
中,点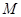 是
是 的中点,
的中点, .
.
(1)求棱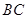 的长;
的长;
(2)求异面直线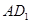 与
与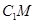 所成角的大小.
所成角的大小.
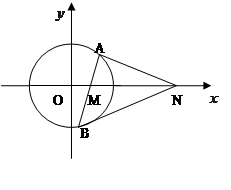
(本小题满分16分)如图,已知圆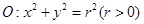 ,动直线
,动直线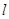 过点
过点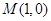 交圆
交圆 于
于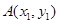 ,
, 两点(点
两点(点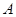 在
在 轴上方),点
轴上方),点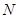 在
在 轴上,若点
轴上,若点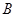 的坐标为
的坐标为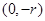 ,则点
,则点 的横坐标为
的横坐标为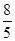 .
.
(1)求 的值;
的值;
(2)当直线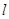 的斜率为
的斜率为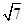 时,直线
时,直线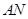 与圆
与圆 相切,求点
相切,求点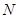 的坐标;
的坐标;
(3)试问:是否存在一定点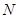 ,使得
,使得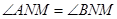 总成立?若存在,请求出点
总成立?若存在,请求出点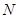 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.