菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.
试问小华选择哪种方案更优惠,请说明理由.
如图,AC=AD,∠BAC=∠BAD,点E在AB上.
.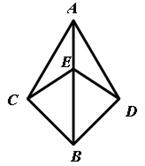
你能找出 对全等的三角形
请写出一对全等三角形,并说明理由
在下列三个二元一次方程中,请你选择合适的两个方程组成二元一次方程组,然后求出方程组的解.可供选择的方程:① y=2x-3② 2x+y=5③ 4x-y=7.
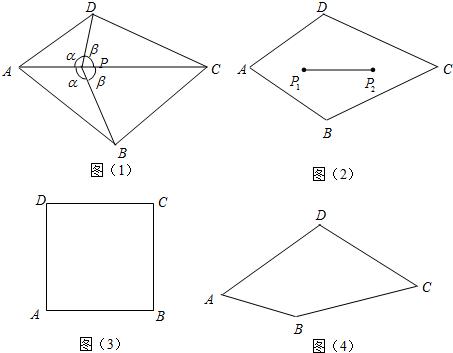
如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
书籍是人类进步的阶梯!为爱护书一般都将书本用封皮包好.
问题1:现有精装词典长、宽、厚尺寸如图(1)所示(单位:cm),若按图(2)的包书方式,将封面和封底各折进去3cm.试用含a、b、c的代数式分别表示词典封皮(包书纸)的长是2b+c+6cm,宽是acm;
问题2:在如图(4)的矩形包书纸皮示意图中,虚线为折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长即为折叠进去的宽度.若有一数学课本长为26cm、宽为18.5cm、厚为1cm,小海宝用一张面积为1260cm2的矩形纸包好了这本数学书,封皮展开后如图(4)所示.若设正方形的边长(即折叠的宽度)为xcm,则包书纸长为2x+38cm,宽为2x+26cm(用含x的代数式表示).
请帮小海宝列好方程,求出第(1)题中小正方形的边长xcm.
光明中学九(1)班的一个课外活动小组参加社会实践,他们到人民路口调查进入人民东路的车流量情况,下表是他们的调查记载表.
光明中学社会实践调查记载表
| 车辆类型 |
“正”字记录 |
辆数 |
占总车流量的百分比 |
| 公交车 |
正正正正正正 |
32 |
17.3% |
| 货车 |
正正正正正正正 |
39 |
21.1% |
| 小轿车 |
正正正正正正正正正正正正正正 |
74 |
 |
| 摩托车 |
正正正 |
18 |
9.7% |
| 其他 |
正正正正 |
22 |
11.9% |
| 合计 |
185 |
100% |
请你根据表中数据,解答下列问题:表中有一处数据被墨汁污染,写出被污染处的数:%,并补全下面的车流量频数分布直方图;
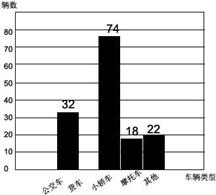
由经验估计可知,在所调查的时段内,每增加投放1辆公交车,可减少8辆小轿车.为了使该时段内,小轿车的流量减少到只比公交车多15辆,问公交公司应增加投放多少辆公交车?