如图，⊙C的内接⊿AOB中，AB=AO=4,tan∠AOB=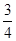
,抛物线y=ax2+bx经过点A(4，0)与点（-2，6）
（1）求抛物线的函数解析式．
（2）直线m与⊙C相切于点A交y轴于点D，动点P在线段OB上，从点O出发向点B运动;同时动点Q在线段DA上，从点D出发向点A运动，点P的速度为每秒1个单位长，点Q的速度为每秒2个单位长，当PQ⊥AD时,求运动时间t的值
（3）点R在抛物线位于x轴下方部分的图象上，当⊿ROB面积最大时，求点R的坐标.
操作与思考：
操作：将长为1，宽为
的长方形纸片（
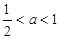），如图那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．如此反复操作下去，若在第n次操作后剩下的长方形是正方形，则操作终止．
思考：
（1）第一次操作后，剩下的长方形的边长分别为 、 ．（用含的式子表示）
（2）如果第二次操作后剩下的长方形恰好是正方形，则的值是 ．
（3）第三次操作后，若剩下的长方形恰好是正方形，试求的值．
生态公园计划在园内的坡地上种植一片有A、B两种树的混合林，需要购买这两种树苗共100棵．假设这批树苗种植后成活95棵，种植A、B两种树苗的相关信息如下表：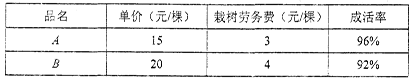
（1）求购买这两种树苗各多少棵？
（2）求种植这片混合林的总费用需多少元？
某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下．（单位：km）
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| －4 |
＋7 |
－9 |
＋8 |
＋6 |
－5 |
－4 |
（1）求收工时，检修小组在A地的哪个方向？距离A地多远？
（2）在第几次纪录时距A地最远？
（3）若汽车行驶每千米耗油0．2升，问从A地出发，检修结束后再回到A地共耗油多少升？
先化简，再求值：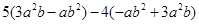
，其中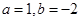
．
解方程：
（1）
（2）