(本小题满分16分)
已知数列{an}的前n项和为Sn,且Sn=2an-2n+1,nÎN*.
(1)求数列{an}的通项公式;
(2)设bn= log2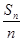 ,Tn=
,Tn= +
+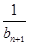 +
+ +…+
+…+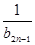 ,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>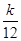 恒成立?若存在,求出k的值;若不存在,请说明理由.
恒成立?若存在,求出k的值;若不存在,请说明理由.
(本小题满分14分)设函数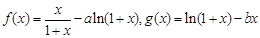 .
.
(1)若函数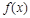 在
在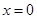 处有极值,求函数
处有极值,求函数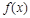 的最大值;
的最大值;
(2)①是否存在实数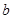 ,使得关于
,使得关于 的不等式
的不等式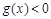 在
在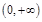 上恒成立?若存在,求出
上恒成立?若存在,求出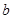 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式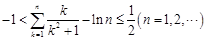 .
.
(本小题满分14分)某商场预计2015年从1月起前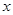 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量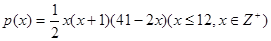 (单位:件)
(单位:件)
(1)写出第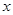 个月的需求量
个月的需求量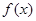 的表达式;
的表达式;
(2)若第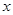 个月的销售量
个月的销售量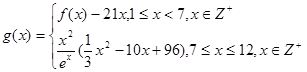 (单位:件),每件利润
(单位:件),每件利润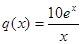 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: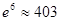 )
)
(本小题满分12分)已知函数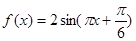
(1)当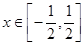 时,求
时,求 的最值;
的最值;
(2)若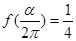 ,求
,求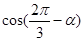 的值
的值
(本小题满分12分)已知数列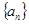 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,且满足
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,且满足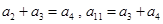 ,记
,记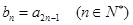
(1)求数列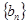 的通项公式;
的通项公式;
(2)设数列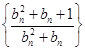 的前
的前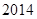 项和为
项和为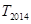 .求不超过
.求不超过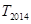 的最大整数.
的最大整数.
(本小题满分12分)已知向量 函数
函数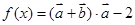
(1)求函数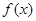 的最小正周期
的最小正周期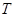 ;
;
(2)已知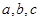 分别为
分别为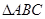 内角
内角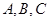 的对边,其中
的对边,其中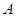 为锐角,
为锐角,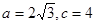 ,且
,且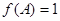 ,求
,求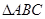 的面积
的面积