已知等腰 中,
中,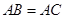 ,
,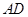 平分
平分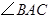 交
交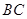 于
于 点,在线段
点,在线段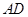 上任取一点
上任取一点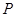 (
(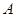 点除外),过
点除外),过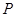 点作
点作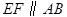 ,分别交
,分别交 于
于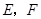 点,作
点,作 ,交
,交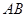 于
于 点,连结
点,连结 .
.
(1)求证:四边形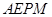 为菱形;
为菱形;
(2)当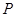 点在何处时,菱形
点在何处时,菱形 的面积为四边形
的面积为四边形 面积的一半?
面积的一半?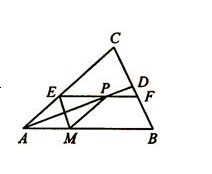
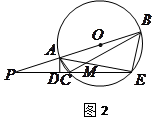
如图1,线段 过圆心
过圆心 ,交圆
,交圆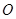 于
于 两点,
两点,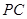 切圆
切圆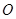 于点
于点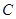 ,作
,作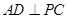 ,垂足为
,垂足为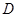 ,连结
,连结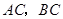 .
.
(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线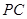 变为图2中割线
变为图2中割线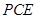 的情形,
的情形,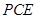 与圆
与圆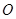 交于
交于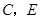 两点,
两点, 与
与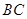 交于点
交于点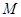 ,
,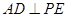 ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外);
(3)在图2中,证明: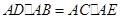 .
.
蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间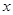 (月份)与市场售价
(月份)与市场售价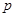 (元/千克)的关系如下表:
(元/千克)的关系如下表:
上市时间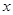 (月份) (月份) |
1 |
2 |
3 |
4 |
5 |
6 |
市场售价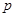 (元/千克) (元/千克) |
10.5 |
9 |
7.5 |
6 |
4.5 |
3 |
这种蔬菜每千克的种植成本 (元/千克)与上市时间
(元/千克)与上市时间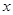 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价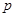 (元/千克)关于上市时间
(元/千克)关于上市时间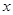 (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过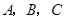 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
如图,某居民小区内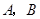 两楼之间的距离
两楼之间的距离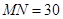 米,两楼的高都是20米,
米,两楼的高都是20米,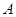 楼在
楼在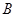 楼正南,
楼正南,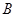 楼窗户朝南.
楼窗户朝南.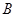 楼内一楼住户的窗台离小区地面的距离
楼内一楼住户的窗台离小区地面的距离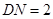 米,窗户高
米,窗户高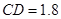 米.当正午时刻太阳光线与地面成
米.当正午时刻太阳光线与地面成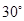 角时,
角时, 楼的影子是否影响
楼的影子是否影响 楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.
楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.
(参考数据: ,
, ,
,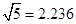 )
)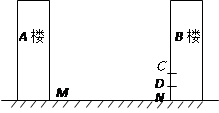
为改善办学条件,北海中学计划购买部分 品牌电脑和
品牌电脑和 品牌课桌.第一次,用9万元购买了
品牌课桌.第一次,用9万元购买了 品牌电脑10台和
品牌电脑10台和 品牌课桌200张.第二次,用9万元购买了
品牌课桌200张.第二次,用9万元购买了 品牌电脑12台和
品牌电脑12台和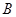 品牌课桌120张.
品牌课桌120张.
(1)每台 品牌电脑与每张
品牌电脑与每张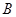 品牌课桌的价格各是多少元?
品牌课桌的价格各是多少元?
(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买 品牌电脑35台以上(含35台),按九折销售,一次购买
品牌电脑35台以上(含35台),按九折销售,一次购买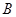 品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?