蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间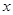 (月份)与市场售价
(月份)与市场售价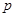 (元/千克)的关系如下表:
(元/千克)的关系如下表:
上市时间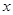 (月份) (月份) |
1 |
2 |
3 |
4 |
5 |
6 |
市场售价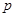 (元/千克) (元/千克) |
10.5 |
9 |
7.5 |
6 |
4.5 |
3 |
这种蔬菜每千克的种植成本 (元/千克)与上市时间
(元/千克)与上市时间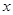 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价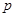 (元/千克)关于上市时间
(元/千克)关于上市时间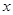 (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过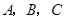 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
已知 边形的内角和 .
(1)甲同学说, 能取 ;而乙同学说, 也能取 .甲、乙的说法对吗?若对,求出边数 .若不对,说明理由;
(2)若 边形变为 边形,发现内角和增加了 ,用列方程的方法确定 .
如图,点 , , , 在直线 上 , 之间不能直接测量),点 , 在 异侧,测得 , , .
(1)求证: ;
(2)指出图中所有平行的线段,并说明理由.


请你参考黑板中老师的讲解,用运算律简便计算:
(1)
(2) .
如图1, 中, ,点 为边 上一点, 于点 .点 为 中点, 的延长线交 于点 .
(1)求证: ;
(2)若 ,求 的大小;
(3)如图2,若 ,点 为 的中点,求证: .

小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加 盆,第二期盆景与花卉售完后的利润分别为 , (单位:元).
(1)用含 的代数式分别表示 , ;
(2)当 取何值时,第二期培植的盆景与花卉售完后获得的总利润 最大,最大总利润是多少?