小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆．售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元．调研发现：
①盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；
②花卉的平均每盆利润始终不变．
小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加盆，第二期盆景与花卉售完后的利润分别为，（单位：元）．
（1）用含的代数式分别表示，；
（2）当取何值时，第二期培植的盆景与花卉售完后获得的总利润最大，最大总利润是多少？
△ABC在平面直角坐标系中的位置如图所示.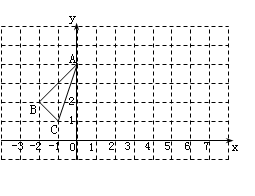 
作出△ABC关于
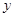轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；
观察△A1B1C1和△A2B2C2，它们是否关于某直线对称？若是，请在图上画出这条对称轴.
化简并求值：已知：
，求
的值.
解不等式组：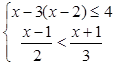
.
直线
＝
（k≠0）与坐标轴分别交于A、B两点，OA、OB的长分别
是方程
＝0的两根（OA＞OB）．动点P从O点出发，沿路线O→B→A以每
秒1个单位长度的速度运动，到达A点时运动停止．直接写出A、B两点的坐标；
设点P的运动时间为t(秒)，△OPA的面积为S，求S与t之间的函数关系式；
当S＝12时，求出点P的坐标，此时，在坐标轴上是否存在点M，使以O、A、
P、M为顶点的四边形是梯形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数
（台）与补贴款额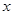
（元）之间大致满足如图①所示的一次函数关系．随着补贴款额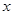的不断增大，销售量也不断增加，但每台彩电的收益
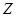（元）会相应降低且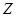与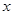之间也大致满足如图②所示的一次函数关系．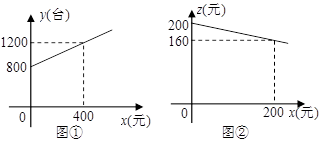
在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？
在政府补贴政策实施后，分别求出该商场销售彩电台数
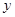和每台家电的收益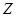与政府补贴款额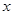之间的函数关系式；要使该商场销售彩电的总收益
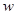（元）最大，政府应将每台补贴款额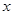定为多少？并求出总收益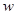的最大值．