如图，在平面直角坐标系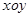
中，已知抛物线经过点Ａ(0，4)，B(1，0)，C（5，0），抛物线对称轴
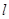与
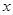轴相交于点M．
（1）求抛物线的解析式和对称轴；
（2）设点P为抛物线（
）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
正整数，请你直接写出点P的坐标；
（3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求
出点N的坐标；若不存在，请你说明理由． 
若x+y=2，且(x+2)(y+2)=5，求x2+xy+y2的值．
如图，如果AC=BD，AE∥CF，AE=CF，那么BE∥DF吗，请说明理由。
解方程组：
先化简，再求值(x+2)2-2(x+2)(x－4)+(x－3)(x+3)；其中x=－l
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣4，0），点B的坐标是（0，b）（b＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P´（点P´不在y轴上），连接PP´，P´A，P´C．设点P的横坐标为a．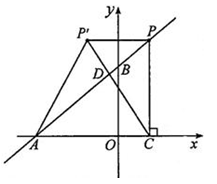
（1）当b=3时，
①求直线AB的解析式；
②若点P′的坐标是（﹣1，m），求m的值；
（2）若点P在第一象限，记直线AB与P´C的交点为D．当P´D：DC=1：3时，求a的值；
（3）是否同时存在a，b，使△P´CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．