如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕点M顺时针旋转90°得到线段NM,在CD边上取点P,使CP=BM,连接NP,BP,设线段MN与CD交于点Q,连接AQ.
(1)求证:四边形BMNP是平行四边形.
(2)若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.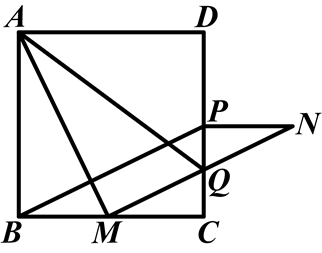
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.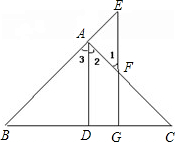
理由如下:∵AD⊥BC于D,EG⊥BC于G,( 已知 )
∴∠ADC=∠EGC=90°,()
∴AD∥EG,( )
∴∠1=∠2,( )
=∠3,( )
又∵∠E=∠1,()
∴∠2=∠3 ( )
∴AD平分∠BAC.( )
解不等式组: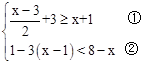 .同时写出不等式组的整数解。
.同时写出不等式组的整数解。
因式分解:(1)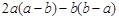 ;(2)
;(2)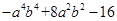
计算或化简:(1)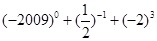 ;(2)
;(2)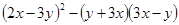
在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度(0<α≤180°)得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于P、Q.
(1)四边形OABC的形状是 , ;
;
(2)①如图1,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求PQ的长;
②如图2,当四边形OA′B′C′的顶点B′落在直线BC上时,求PQ的长.
(3)小明在旋转中发现,当点P位于点B的右侧时,总存在线段PQ与线段相等;同时存在着特殊情况 ,求出此时P点的坐标。
,求出此时P点的坐标。