四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.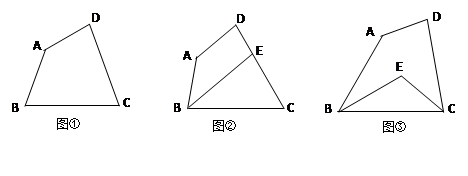
已知:如图, , 相交于点 , , .
求证:(1) ;
(2) .

计算:
(1) ;
(2) .
如图,抛物线 与 轴交于 , ,与 轴交于点 .连接 , ,点 在抛物线上运动.
(1)求抛物线的表达式;
(2)如图①,若点 在第四象限,点 在 的延长线上,当 时,求点 的坐标;
(3)如图②,若点 在第一象限,直线 交 于点 ,过点 作 轴的垂线交 于点 ,当 为等腰三角形时,求线段 的长.

已知正方形 与正方形 ,正方形 绕点 旋转一周.
(1)如图①,连接 、 ,求 的值;
(2)当正方形 旋转至图②位置时,连接 、 ,分别取 、 的中点 、 ,连接 、试探究: 与 的关系,并说明理由;
(3)连接 、 ,分别取 、 的中点 、 ,连接 , ,请直接写出线段 扫过的面积.

一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离 与慢车行驶的时间 之间的关系如图:
(1)快车的速度为 , 点的坐标为 .
(2)慢车出发多少小时后,两车相距 .
