如图,已知A(-4,2)、B(n,-4)是一次函数 的图象与反比例函数
的图象与反比例函数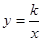 的图象的两个交点.
的图象的两个交点.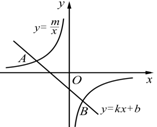
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△ABO的面积。
如图,把质地均匀的A、B两个转盘都分成三等分,玲玲和兰兰利用它们做游戏,同时自由转动两个转盘,当两个指针所停区域(停在分界线上重转)的数都是奇数或都是偶数时,则玲玲获胜,当两个指针所停区域的数是一奇一偶时,则兰兰获胜,列表或画树状图,用概率的知识说明这个游戏对她们是否公平?
计算:
研究下列算式,你会发现什么规律?



……
问题探究
(1)请你找出规律并计算 =_____________=( )
=_____________=( ) .
.
(2)用含有 的式子表示上面的规律:_____________________________.
的式子表示上面的规律:_____________________________.
问题解决
(3)用找到的规律解决下面的问题:
计算:  =_______________.
=_______________.
写出运算过程:
(1)用小立方块搭成的几何体,主视图和俯视图如下图,问搭成这样的几何体最多要小立方块,最少要小立方块.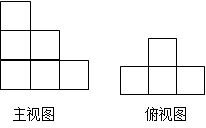
(2)世园会期间,西安某学校组织教师和学生参观世园会,每位教师的车费为m元,每位学生的车费为n元,学生每满100人可优惠2人的车费,如果该校七年级有教师20人,学生612人,则需要付给汽车公司的总费用为_______元.