如图，已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C， D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3∶2．
（1）求这条抛物线对应的函数关系式；
（2）连结BD，试判断BD与AD的位置关系，并说明理由；
（3）连结BC交直线AD于点M，在直线AD上，是否存在这样的点N（不与点M重合），使得以A、B、N为顶点的三角形与△ABM相似？若存在，请求出点N的坐标；若不存在，请说明理由．
如图，已知四边形ABCD是平行四边形，点E、B、D、F在同一直线上，且BE=DF．求证：AE=CF．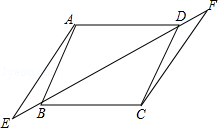
某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援．当飞机到达距离海面3000米的高空C处，测得A处渔政船的俯角为60°，测得B处发生险情渔船的俯角为30°，请问：此时渔政船和渔船相距多远？（结果保留根号）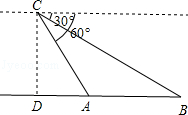
我市党的群众路线教育实践活动不断推进并初见成效．某县督导小组为了解群众对党员干部下基层、查民情、办实事的满意度（满意度分为四个等级：
| A．非常满意； | B．满意； | C．基本满意； | D．不满意），在某社区随机抽样调查了若干户居民，并根据调查数据绘制成下面两个不完整的统计图． |
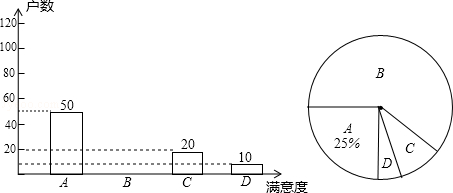
请你结合图中提供的信息解答下列问题．
（1）这次被调查的居民共有户；
（2）请将条形统计图补充完整．
（3）若该社区有2000户居民，请你估计这个社区大约有多少户居民对党员干部的满意度是“非常满意”．根据统计结果，对党员干部今后的工作有何建议？
已知直线l平行于直线y=2x+1，并与反比例函数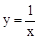
的图象相交于点A（a，1），求直线l的解析式．
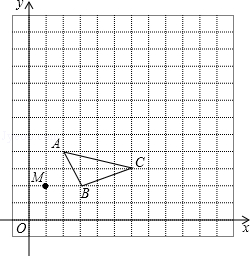
在13×13的网格图中，已知△ABC和点M（1，2）．
（1）以点M为位似中心，位似比为2，画出△ABC的位似图形△A′B′C′；
（2）写出△A′B′C′的各顶点坐标．