如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.
(1)用含t的式子表示点E的坐标为_______;
(2)当t为何值时,∠OCD=180°?
(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.
如图,∠1=∠2,AC平分∠DAB,求证:DC∥AB.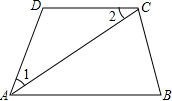
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.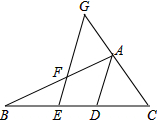
看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:∵∠1=35°,∠2=35°(已知),
∴∠1=∠2
∴_______∥_______(同位角相等,两条直线平行)
又∵AC⊥AE(已知),
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=_______°(等式的性质)
同理可得,∠FBD+∠2=_______°
∴_______∥_______(同位角相等,两条直线平行)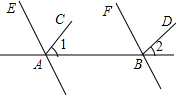
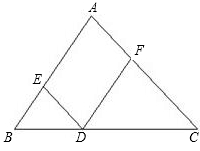
完成下列解答过程:
证明:(1)∵∠A=_______,(已知)
∴AC∥ED.(_______)
(2)∵∠EDF=_______,(已知)
∴AC∥ED.(_______)
(3)∵∠A+∠DFA=180°(已知)
∴_______∥_______.(_______)
如图,已知a∥b,∠3+∠2=180°,b与c平行吗?说明理由.