因式分解:9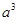 +6
+6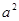 b+a
b+a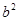 .
.
计算:(x﹣2)(x+5)﹣x(x﹣2).
如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.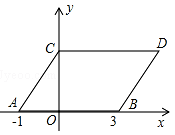
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1.
∴y>﹣1.
又∵y<0,∴﹣1<y<0.…①
同理得:1<x<2. …②
由①+②得﹣1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x﹣y=4,且x>3,y<1,则x+y的取值范围是.
(2)已知y>1,x<﹣1,若x﹣y=m成立,求x+y的取值范围(结果用含m的式子表示).
为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>0)支钢笔需要花y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.