已知：抛物线
（a≠0）的顶点M的坐标为（1,－2）与y轴交于点C（0，
），与x轴交于A、B两点（A在B的左边）.
（1）求此抛物线的表达式；
（2）点P是线段OB上一动点（不与点B重合），点Q在线段BM上移动且∠MPQ＝45°，设线段OP＝x，MQ＝
1，求y1与x的函数关系式，并写出自变量x的取值范围；
（3）①在（2）的条件下是否存在点P，使△PQB是PB为底的等腰三角形，若存在试求点Q的坐标，若不存在说明理由；
②在（1）中抛物线的对称轴上是否存在点F，使△BMF是等腰三角形，若存在直接写出所有满足条件的点F的坐标.
解分式方程：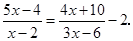
现有甲、乙两种金属的合金10kg，如果加入甲种金属若干，那么重新熔炼后的合金中乙种金属占2份，甲种金属占3份，如果加入的甲种金属是第一次加入的2倍，那么重新熔炼后的合金中乙种金属占3份，甲种金属占7份，第一次加入的甲种金属多少？原来这块合金中甲种金属的百分比是多少？
先化简，再求值：
，其中x=
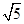+2．
解不等式组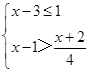
．
【回归课本】我们曾学习过一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例．
【初步体验】
（1）如图1，在△ABC中，点D、F在AB上，E、G在AC上，DE∥FC∥BC．若AD=2，AE=1，DF=6，则EG= ，
= ．
（2）如图2，在△ABC 中，点D、F在AB上，E、G在AC上，且DE∥BC∥FG．以AD、DF、FB为边构造△ADM（即AM=BF，MD=DF）；以AE、EG、GC为边构造△AEN（即AN=GC，NE=EG）．求证：∠M=∠N．
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题：
（3）如图3，已知△ABC和线段a，请用直尺与圆规作△A′B′C′．满足：①△A′B′C′∽△ABC；②△A′B′C′的周长等于线段a的长度．（保留作图痕迹，并写出作图步骤）