如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.
某文化用品商店计划同时购进一批A、B两种型号的计算器,若购进A型计算器10只和B型计算器8只,共需要资金880元;若购进A型计算器2只和B型计算器5只,共需要资金380只。
(1)求A、B两种型号的计算器每只进价各是多少元?
(2)该经销商计划购进这两种型号的计算器共50只,而可用于购买这两种型号的计算器的资金不超过2520元,根据市场行情,销售一只A型计算器可获利10元,销售一只B型计算器可获利15元,该经销商希望销售完这两种型号的计算器,所获利润不少于620元,则该经销商有哪几种进货方案?
如图,在△ABC中,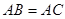 ,以AC为直径的半圆O分别交AB、BC于点D、E
,以AC为直径的半圆O分别交AB、BC于点D、E
(1)求证:点E是BC的中点
(2)若 ,求∠BED的度数。
,求∠BED的度数。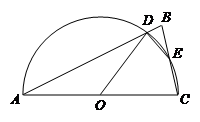
某市教育局为了了解初一学生第一学期参加社会实践活动的天数,随机抽查本市部分初一学生第一学期参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)
请你根据图中提供的信息,回答下列问题:
(1) __________%,并写出该扇形所对圆心角的度数为___________;补全条形图;
__________%,并写出该扇形所对圆心角的度数为___________;补全条形图;
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该市共有初一学生20000人,请你估计“活动时间不少于5天”的大约有多少人?
(1)如图,在平行四边形ABCD中,E为BC中点,AE的延长线与DC的延长线相交于点F,证明:△ABE≌△FCE
(2)如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角 为
为 ,看这栋高楼底部的俯角
,看这栋高楼底部的俯角 为
为 ,热气球与高楼的水平距离
,热气球与高楼的水平距离 ,这栋高楼有多高(
,这栋高楼有多高( ,结果保留小数点后一位)?
,结果保留小数点后一位)?
(1)计算:
(2)先化简,再求值: ,其中
,其中 。
。