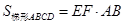(本题6分)某省为解决农村饮用水问题,省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
(1)求证:AC⊥BD
(2)求△AOB的面积
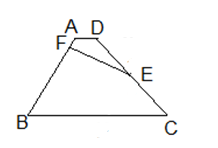
如图某水库大坝的横截面是梯形ABCD,AD∥BC,EF为水面,点E在DC上,测得背水坡AB的长为18米,倾角∠B=300,迎水坡CD上线段DE的长为8米,∠ADC=1200.
(1)请你帮技术员算出水的深度(精确到0.01米,参考数据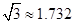 );
);
(2)就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用20天?(精确到0.01米)
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,连接AE、EF、AC,EF和AC相交于点O。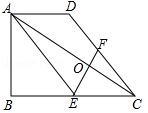
(1)求证:AO·OF=OC·OE;
(2)若点F是DC的中点,连接BD交AE于点G,求证:四边形EFDG是菱形.
如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,求AC的长.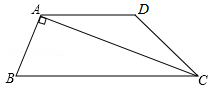
已知,如图,梯形ABCD中,AD∥BC,E为CD中点,EF⊥AB于F
求证: