已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,连接AE、EF、AC,EF和AC相交于点O。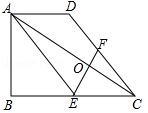
(1)求证:AO·OF=OC·OE;
(2)若点F是DC的中点,连接BD交AE于点G,求证:四边形EFDG是菱形.
作图题:
(1)如图,有两个7×4的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形。请在图①、图②中分别画出一条线段,同时满足以下要求:
①线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
②将梯形分成两个图形,其中一个是轴对称图形;
③图①、图②中分成的轴对称图形不全等。
(2)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站 ,张、李两村座落在两相交公路内(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定
,张、李两村座落在两相交公路内(如图所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定 点的位置.
点的位置.

已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
求证:(1)△ABC≌△DEF;(2)GF=GC。
(要求:写出重要证明依据)
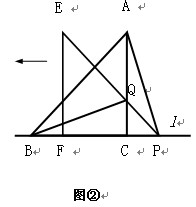
(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。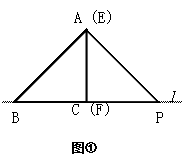
阅读材料,解答下列问题.
例:当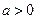 时,如
时,如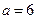 则
则 ,故此时
,故此时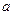 的绝对值是它本身
的绝对值是它本身
当 时,
时, ,故此时
,故此时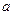 的绝对值是零
的绝对值是零
当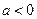 时,如
时,如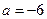 则
则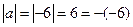 ,故此时
,故此时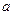 的绝对值是它的相反数
的绝对值是它的相反数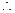 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即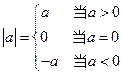
问:(1)这种分析方法涌透了数学思想.
(2)请仿照例中的分类讨论的方法,分析二次根式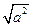 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想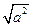 与
与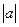 的大小关系.
的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题: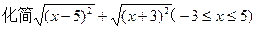
(1)计算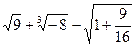
(2)解方程: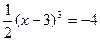
(3)计算: