如图，抛物线y＝(x＋1)2＋k 与x轴交于A、B两点，与y轴交于点C (0，－3)．
（1）求抛物线的对称轴及k的值；
（2）抛物线的对称轴上存在一点P，使得PA＋PC的值最小，求此时点P的坐标；
（3）点M是抛物线上一动点，且在第三象限．当M点运动到何处时，四边形AMCB的面积最大？求出四边形AMCB的最大面积及此时点M的坐标；
（4）若点E在抛物线的对称轴上，抛物线上是否存在点F，使以A，B，E，F为顶点的的四边形为平行四边形？若存在，直接写出出所有满足条件的点F的坐标；若不存在，请说明理由．
如右图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求
（1）△ABC的面积；
（2）△ABC的周长；
（3）点C到AB边的距离．
(6分)如图，某水坝的横断面是梯形，坝顶宽8米，坝高20米，斜坡AD的坡比为
，斜坡BC的坡比为
，求坝底AB的长.
用适当的方法解方程：
（1）
（2）
（3） 
（4）
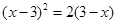
（本题10分）如图，△ABC中，∠A=90º，∠ABC与∠ACB的角平分线交于点I，△ABC的外角∠DBC与∠BCE的角平分线交于P。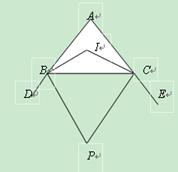
①则∠BIC= ，∠P= （直接写出答案）
②当∠A的度数增加4º时，∠BIC，∠P的度数发生怎样的变化？请说明理由。
（本题8分）如图，已知在四边形ABCD中，∠B=∠D=
，AE、CF分别是∠DAB及∠DCB的平分线．则AE与FC有什么关系？请说明理由。