如图,在平面直角坐标系中,反比例函数 (
(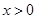 ,
, )的图象经过点
)的图象经过点 (1,2),
(1,2),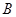 (
(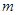 ,
,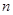 )(
)(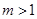 ),过点B作
),过点B作 轴的垂线,垂足为C.
轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为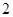 时,求点B的坐标;
时,求点B的坐标;
(3)在(2)的情况下,直线y=ax-1过线段AB上一点P(P不与A、B重合),求a的取值范围.
如图,有四张背面完全相同的纸牌 A、 B、 C、 D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用 A、 B、 C、 D表示).
如图,海中有一个小岛 A,它周围8海里内有暗礁.渔船跟踪鱼群由西向东航行,在 B点测得小岛 A在北偏东60°方向上,航行10海里到达 C点,这时测得小岛 A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?

已知,如图,抛物线 y= ax 2+ bx+ c( a≠0)的顶点为 M(1,9),经过抛物线上的两点 A(﹣3,﹣7)和 B(3, m)的直线交抛物线的对称轴于点 C.
(1)求抛物线的解析式和直线 AB的解析式.
(2)在抛物线上 A、 M两点之间的部分(不包含 A、 M两点),是否存在点 D,使得 S △ DAC=2 S △ DCM?若存在,求出点 D的坐标;若不存在,请说明理由.
(3)若点 P在抛物线上,点 Q在 x轴上,当以点 A, M, P, Q为顶点的四边形是平行四边形时,直接写出满足条件的点 P的坐标.

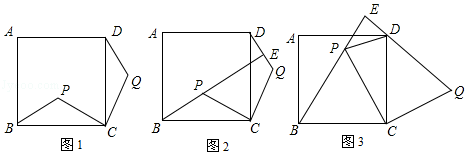
如图,点 P是正方形 ABCD内的一点,连接 CP,将线段 CP绕点 C顺时针旋转90°,得到线段 CQ,连接 BP, DQ.
(1)如图1,求证:△ BCP≌△ DCQ;
(2)如图,延长 BP交直线 DQ于点 E.
①如图2,求证: BE⊥ DQ;
②如图3,若△ BCP为等边三角形,判断△ DEP的形状,并说明理由.
当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量 y(本)与销售单价 x(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠 a(0< a≤6)元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 a的值.