已知：如图1，△OAB是边长为2的等边三角形，OA在x轴上，点B在第一象限内；△OCA是一个等腰三角形，OC＝AC，顶点C在第四象限，∠C＝120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个单位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→O→B运动，当其中一个点到达终点时，另一个点也随即停止．
（1）求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；
（2）在OA上（点O、A除外）存在点D，使得△OCD为等腰三角形，请直接写出所有符合条件的点D的坐标；
（3）如图2，现有∠MCN＝60°，其两边分别与OB、AB交于点M、N，连接MN．将∠MCN绕着C点旋转（0°＜旋转角＜60°），使得M、N始终在边OB和边AB上．试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．
先化简，再求值．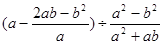
其中b=1，－3＜a＜
且a为整数
（1）解不等式组．并把解集在数轴上表示出来．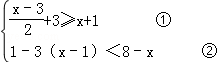
．
（2）阅读某同学解分式方程的具体过程，回答后面问题．
解方程
．
解：原方程可化为：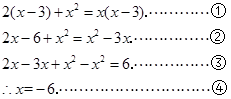
检验：当
时，各分母均不为0，
∴是原方程的解．
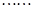⑤
请回答：（1）第①步变形的依据是____________________；
（2）从第____步开始出现了错误，这一步错误的原因是__________________________；
（3）原方程的解为____________________________．
在一次课外实践活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离．现测得AC=30m，BC=70m，∠CAB=120°，请计算A，B两个凉亭之间的距离．
煤炭是攀枝花的主要矿产资源之一，煤炭生产企业需要对煤炭运送到用煤单位所产生的费用进行核算并纳入企业生产计划．某煤矿现有1000吨煤炭要全部运往A．B两厂，通过了解获得A．B两厂的有关信息如下表（表中运费栏“元/t•km”表示：每吨煤炭运送一千米所需的费用）：
| 厂别 |
运费（元/t•km） |
路程（km） |
需求量（t） |
| A |
0.45 |
200 |
不超过600 |
| B |
a（a为常数） |
150 |
不超过800 |
（1）写出总运费y（元）与量x（t）之间函数关系式，写出自变量取值范围；
（2）请你运用函数有关知识，为该煤矿设计总运费最少的运送方案，并求出最少的总运费（可用含a的代数式表示）
已知，如图，A，B分别在x轴和y轴上，且OA=2OB，直线y1=kx+b经过A点与抛物线y2=-x2+2x+3交于B，C两点，
（1）试求k，b的值及C点坐标；
（2）x取何值时y1，y2均随x的增大而增大；
（3）x取何值时y1＞y2．