某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录了6个抽查数据,获得重量数据的茎叶图如图4.
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,
, ,
, ,
,
且 .
.
(1)求角 的值;
的值;
(2)若 为锐角三角形,且
为锐角三角形,且 ,求
,求 的取值范围.
的取值范围.
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),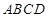 是一个标出为
是一个标出为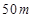 的正方形地皮,扇形
的正方形地皮,扇形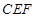 是运动场的一部分,其半径为
是运动场的一部分,其半径为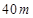 ,矩形
,矩形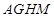 就是拟建的健身室,其中
就是拟建的健身室,其中 分别在
分别在 和
和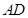 上,
上,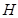 在
在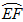 上,设矩形
上,设矩形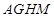 的面积为
的面积为 ,
, .
.
(I)请将 表示为
表示为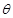 的函数,并指出当点
的函数,并指出当点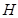 在
在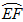 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
(II)由上面函数建立的思想,试求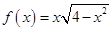 的最大值.
的最大值.
已知函数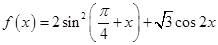 .
.
(I)求函数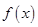 的单调递增区间;
的单调递增区间;
(II)若关于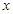 的方程
的方程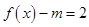 在
在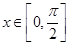 上有两个不同的解,求实数
上有两个不同的解,求实数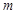 的取值范围.
的取值范围.
已知函数 在区间
在区间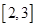 上有最大值4和最小值1,设
上有最大值4和最小值1,设 .
.
(I)求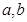 的值;
的值;
(II)若不等式 在
在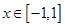 上有解,求实数
上有解,求实数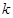 的取值范围.
的取值范围.
已知函数 为偶函数,且
为偶函数,且 的最小值是
的最小值是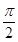 .
.
(I)求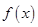 ;
;
(II)用五点法画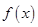 一个周期内的图像.
一个周期内的图像.