(本小题8分)在二项式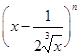 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项的系数;
(3)求展开式中各项的系数和.
已知函数 的部分图象如图所示.
的部分图象如图所示.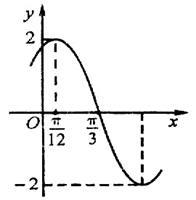
(1)求函数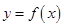 的解析式;
的解析式;
(2)将函数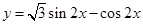 的图象做怎样的平移变换可以得到函数
的图象做怎样的平移变换可以得到函数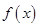 的图象;
的图象;
(3)若方程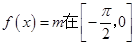 上有两个不相等的实数根,求m的取值范围.
上有两个不相等的实数根,求m的取值范围.
已知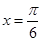 是函数
是函数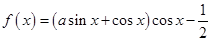 图象的一条对称轴.
图象的一条对称轴.
(1)求a的值;
(2)求函数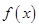 的单调增区间;
的单调增区间;
(3)作出函数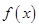 在
在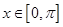 上的图象简图(列表,画图).
上的图象简图(列表,画图).
选修4一5:不等式选讲
已知函数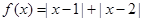 .
.
(1)求关于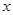 的不等式
的不等式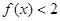 的解集;
的解集;
(2)如果关于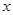 的不等式
的不等式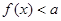 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围.
的取值范围.
选修4一4:坐标系与参数方程
在直角坐标系中,圆 :
: =
= 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线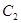 .
.
以坐标原点为极点, 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,
建立极坐标系,直线 的极坐标方程为
的极坐标方程为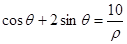 ·
·
(1)求曲线 的直角坐标方程及直线
的直角坐标方程及直线 的直角坐标方程;
的直角坐标方程;
(2)在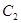 上求一点
上求一点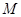 ,使点
,使点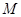 到直线
到直线 的距离最小,并求出最小距离.
的距离最小,并求出最小距离.
选修4一1:几何证明选讲
如图, 是圆
是圆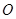 的直径,弦
的直径,弦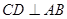 于点
于点 ,
, 是
是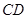 延长线上一点,
延长线上一点,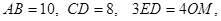
 切圆
切圆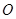 于
于 ,
, 交
交 于
于 .
.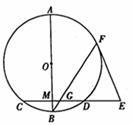
(1)求证: 为等腰三角形;
为等腰三角形;
(2)求线段 的长.
的长.