已知A、B两地相距6千米,上午8∶00,甲从A地出发步行到B地;8∶20后,乙从B地出发
骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示。
(1) 求甲步行的速度是多少?
(2) 求甲、乙二人相遇的时刻?
(3) 求乙到达A地的时刻?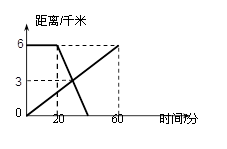
解方程
(1)6x﹣4=3x+2
(2)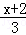 =1+
=1+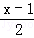 .
.
如图,直线l1的函数关系式为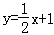 ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
小轿车从甲地出发驶往乙地,同时货车从相距乙地60km的入口处驶往甲地(两车均在甲、乙两地之间的公路上匀速行驶),如图是它们离甲地的路程y(km)与货车行驶时间x(h)之间的函数的部分图象.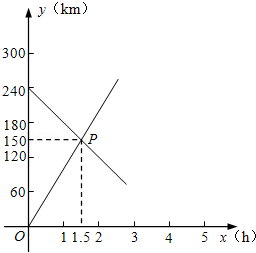
(1)求货车离甲地的路程y(km)与它的行驶时间x(h)的函数关系式;
(2)哪一辆车先到达目的地?说明理由.
我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况,随机抽样调查了实验中学七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).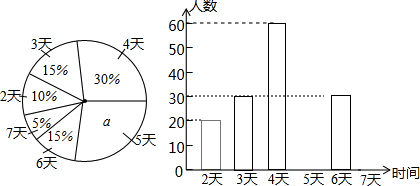
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校七年级学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)如果我市共有七年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
小明从兴化通过申通快递公司给在南京的朋友寄一盒苹果,快递时,他了解到申通快递公司除了收取每次6元的包装费外,苹果不超过2kg收费22元,若超过2kg,则超过的部分按每千克10元收取费用,该公司从兴化到南京快递苹果的费用为y(元),所寄的苹果为x(kg).
(1)求y与x的函数关系式;
(2)已知小明给朋友寄了2.5kg的苹果,请你求出这次快递的费用.