如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
（1）同时自由转动转盘A与B；
（2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针停留在某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5,3×5＝15，按规则乙胜）。
你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由.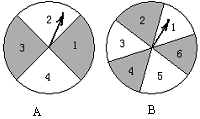
（本小题满分6分）如图，在边长为1个单位长、度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
（1）将△ABC向左平移1个单位，再向上平移5个单位得到△A1B1C1，请画出△A1B1C1；
（2）请在网格中将△ABC以A为位似中心放大 3倍，得△AB2C2，请画出△AB2C2
（本题6分）关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根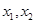
．
（1）求实数k的取值范围．
（2）若方程两实根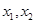满足｜x1｜+｜x2｜=x1·x2，求k的值．
计算或解下列方程：（每题4分，共16分）
（1）sin245°- cos60°+ tan60°·cos230°
（2）
（3）
；
（4）
某公园有一个抛物线形状的观景拱桥ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为 
且过顶点C（0，5）（长度单位：m） 
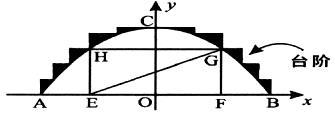
（1）直接写出c的值；
（2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为1．5 m的地毯，地毯的价格为20元／m 2，求购买地毯需多少元?
（3）在拱桥加固维修时，搭建的"脚手架"为矩形EFGH（H、G分别在抛物线的左右侧上），并铺设斜面EG．已知矩形EFGH的周长为27．5m，求点G的坐标．
如图，已知二次函数 
的图象与 
轴交于A、B两点． 
（1）写出A、B两点的坐标（坐标用 
表示）
（2）若二次函数图象的顶点P在以AB为直径的圆上，求二次函数的解析式
（3）设以AB为直径的⊙M与 
轴交于C、D两点，求CD的长．