为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，并从中随机抽取了部分学生成绩（得分取整数，满分为100分）为样本，绘制成统计图（如图所示），请根据统计图提供的信息回答下列问题：
（1）本次测试抽取了 名学生的成绩为样本．
（2）样本中，分数在80～90这一组的频率是 ．
（3）样本的中位数落在 这一小组内．
（4）如果这次测试成绩80分以上（含80分）为优良，那么在抽取的学生中，优良人数为 名；
如果该校有840名学生参加这次竞赛活动，估计优良学生的人数约为 名．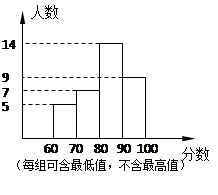
如图，△ABC中，AC=BC，以BC上一点O为圆心，OB为半径作⊙O交AB于点D已知经过点D的⊙O切线恰好经过点C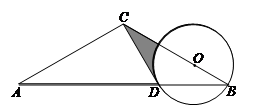
（1）试判断CD与AC的位置关系，并证明；
（2）若△ACB∽△CDB，且AC=3，求图中阴影部分的面积
耘耙是一种清除水稻成长期缝隙间杂草的传统农具，大小款式不一，图1
是其中的一种，图2是其示意图，现测得AC＝40cm，∠C＝30°，∠BAC＝45° 为了使耘耙更加牢固，AB处
常用铁条制成，则制作此耘耙时需准备多长的铁条？（结果保留根号）
在一个袋子中，有完全相同的4张卡片，把它们分别编号为l，2，3，4
（1）从袋子中随机取两张卡片 求取出的卡片编号之和等于4的概率：
（2）先从袋子中随机取一张卡片，记该卡片的编号为a，然后将其放回，再从袋中随机取出一张卡片，级
该卡片的编号为b，利用画树状图或表格求满足a+1＞b的概率
无锡市某中学为了解学生的课外阅读情况 就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学仅选一项），并根据调查结果制作了尚不完整的频数分布表：
| 类别 |
频数（人数） |
频率 |
| 文学 |
m |
0 42 |
| 艺术 |
22 |
0 11 |
| 科普 |
66 |
n |
| 其他 |
28 |
|
| 合计 |
1 |
（1）表中m＝，n＝；
（2）在这次抽样调查中，最喜爱阅读哪类读物的学生最多? 最喜爱阅读哪类读物的学生最少?
（3）根据以上调查，试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?
（每小题4分，共8分）
（1）解方程：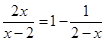
；
（2）解不等式组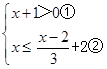
，并写出最小整数解