如图，在△ABC中，∠C=90°，BC=8，AB=10，O为BC上一点，以O为圆心，OB为半径作半圆与BC边、AB边分别交于点D、E，连接DE。
（1）若BD=6，求线段DE的长；
（2）过点E作半圆O的切线，交AC于点F，
证明：AF=EF。
某工厂家具车间造A、B型两类桌子，每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时，漆工油漆一张A、B型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张A、B型桌子分别获利润2千元和3千元，试问工厂每天应生产A、B型桌子各多少张，才能获得利润最大？
如果方程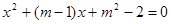
的两个实根一个小于‒1，另一个大于0，求实数m的取值范围
在△ABC中，角A、B、C对边分别为a、b、c。求证：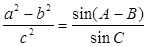
函数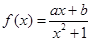
是定义在
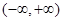上的奇函数，且
.
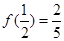（1）求实数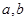
的值.（2）用定义证明
在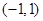
上是增函数；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值（无需说明理由）
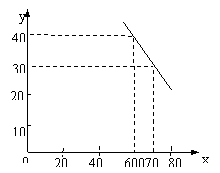
某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价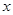
（元/件），可近似看做一次函数
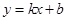的关系（如下图所示）.
（1）根据图象，求一次函数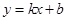的表达式；
（2）设公司获得的毛利润（毛利润＝销售总价－成本总价）为S元,
①求S关于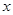的函数表达式；
②求该公司可获得的最大毛利润，并求出相应的销售单价.