某大楼共5层，4个人从第一层上电梯，假设每个人都等可能地在每一层下电梯，并且他们下电梯与否相互独立. 又知电梯只在有人下时才停止.
（Ⅰ）求某乘客在第
层下电梯的概率
；
（Ⅱ）求电梯在第2层停下的概率；
（Ⅲ）求电梯停下的次数
的数学期望.
（1）推导点到直线的距离公式；
（2）已知直线
：
和
：
互相平行，求实数
的值.
如图，直线AB为圆O的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.
(1)证明：DB＝DC；
(2)设圆的半径为1，BC＝
，延长CE交AB于点F，求△BCF外接圆的半径．
如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E.
(1)求证：AB2＝DE·BC；
(2)若BD＝9，AB＝6，BC＝9，求切线PC的长．
如图，已知在△ABC中，AB＝AC，D是△ABC外接圆劣弧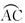
上的点(不与点A，C重合)，延长BD至E.
(1)求证：AD的延长线平分∠CDE；
(2)若∠BAC＝30°，△ABC中BC边上的高为2＋
，求△ABC外接圆的面积．
如图，过圆O外一点M作它的一条切线，切点为A，过A点作直线AP垂直直线OM，垂足为P.
(1)证明：OM·OP＝OA2；
(2)N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点．过B点的切线交直线ON于K.证明：∠OKM＝90°.