平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别为(0，3)、(-1，0)，将此平行四边形绕点0顺时针旋转90°，得到平行四边形
。
(1)若抛物线过点C，A，
，求此抛物线的解析式；
(2)求平行四边形ABOC和平行四边形重叠部分△
的周长；
(3)点M是第一象限内抛物线上的一动点，间：点M在何处时△
的面积最大?最大面积是多少?并求出此时点M的坐标。
（河池）如图，在△ABC中，∠ACB=90°，AC=BC=AD．
（1）作∠A的平分线交CD于E；
（2）过B作CD的垂线，垂足为F；
（3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．
（桂林）如图，△ABC各顶点的坐标分别是A（﹣2，﹣4），B（0，﹣4），C（1，﹣1）．
（1）在图中画出△ABC向左平移3个单位后的△A1B1C1；
（2）在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2；
（3）在（2）的条件下，AC边扫过的面积是 ．
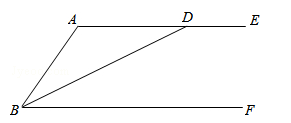
（贵港）如图，已知△ABC三个顶点坐标分别是A（1，3），B（4，1），C（4，4）．
（1）请按要求画图：①画出△ABC向左平移5个单位长度后得到的△A1B1C1；
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2．
（2）请写出直线B1C1与直线B2C2的交点坐标．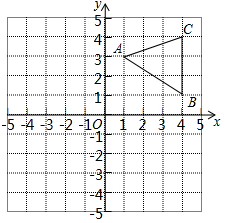
（崇左）如图，△A1B1C1是△ABC向右平移四个单位长度后得到的，且三个顶点的坐标分别为A1（1，1），B1（4，2），C1（3，4）．
（1）请画出△ABC，并写出点A、B、C的坐标；
（2）求出△AOA1的面积．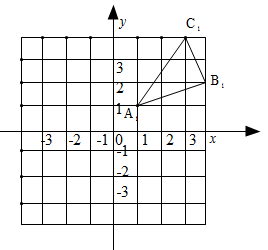
（北海）如图，已知BD平分∠ABF，且交AE于点D，
（1）求作：∠BAE的平分线AP（要求：尺规作图，保留作图痕迹，不写作法）；
（2）设AP交BD于点O，交BF于点C，连接CD，当AC⊥BD时，求证：四边形ABCD是菱形．