一个暗箱里放着6个黑球、4个白球.(每个球的大小和质量均相同)
(1)不放回地依次取出2个球,若第1次取出的是白球,求第2次取到黑球的概率;
(2)有放回地依次取出2个球,求两球颜色不同的概率;
(3)有放回地依次取出3个球,求至少取到两个白球的概率.
(本小题满分10分)选修4-1:几何证明选讲
如图,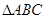 为圆的内接三角形,
为圆的内接三角形,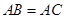 ,
,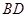 为圆的弦,且
为圆的弦,且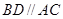 ,过点
,过点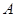 作圆的切线与
作圆的切线与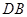 的延长线交于点
的延长线交于点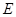 ,
, 与
与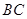 交于点
交于点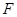 .
.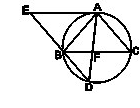
(1)求证:四边形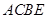 为平行四边形;
为平行四边形;
(2)若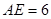 ,
,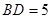 ,求线段
,求线段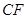 的长.
的长.
已知函数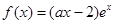 在
在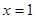 处取得极值.
处取得极值.
(1)求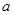 的值;
的值;
(2)求函数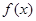 在
在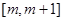 上的最小值;
上的最小值;
(3)求证:对任意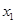 、
、 ,都有
,都有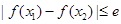 .
.
已知椭圆 的离心率是
的离心率是 ,其左、右顶点分别为
,其左、右顶点分别为 、
、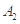 ,
, 为短轴的一个端点,
为短轴的一个端点,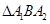 的面积为
的面积为 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与
与 轴交于
轴交于 ,
, 是椭圆
是椭圆 上异于
上异于 、
、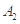 的动点,直线
的动点,直线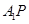 、
、 分别交直线
分别交直线 于
于 、
、 两点,求证:
两点,求证: 为定值.
为定值.
如图,四棱柱 的底面为菱形,
的底面为菱形, ,
, 交于点
交于点 ,
, 平面
平面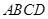 ,
, ,
, .
.
(1)证明: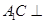 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
在 中,内角
中,内角 、
、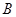 、
、 所对的边分别为
所对的边分别为 ,
, ,
, ,
,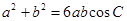 ,且
,且 .
.
(1)求角 的值;
的值;
(2)设函数 ,且
,且 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为 ,求
,求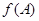 的取值范围.
的取值范围.