(本小题满分12分)
已知斜三棱柱ABC—A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且 , M是A1B1的中点,
, M是A1B1的中点,

(1)求证: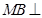 平面ABC;
平面ABC;
(2)求二面角A1—BB1—C的余弦值。
(本小题满分12分)已知二次函数 ,当
,当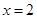 时函数取最小值-1,且
时函数取最小值-1,且
(1)求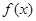 的解析式;
的解析式;
(2)若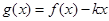 在区间
在区间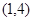 上不单调,求实数
上不单调,求实数 的取值范围.
的取值范围.
(本小题满分10分)已知 ,分别求
,分别求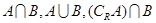 .
. ,
, ,
,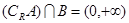
(本小题满分12分)已知函数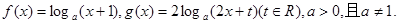
(Ⅰ)若1是关于x的方程 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ)当 时,解不等式
时,解不等式 ;
;
(Ⅲ)若函数 在区间
在区间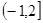 上有零点,求t的取值范围.
上有零点,求t的取值范围.
(本小题满分10分)已知函数 (a>0,且a≠1),
(a>0,且a≠1), =
= .
.
(1)函数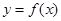 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;
(2)若函数 的图像过点(2,
的图像过点(2,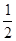 ),证明:方程
),证明:方程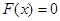 在
在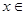 (1,2)上有唯一解.
(1,2)上有唯一解.
(本小题满分12分).如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上.已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.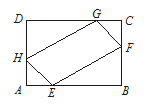
(1)写出y关于x的函数解析式,并求出它的定义域;
(2)当AE为何值时,绿地面积y最大?并求出最大值。