(本小题满分12分)
已知函数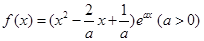
(I)当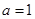 时,求函数
时,求函数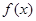 的图象在点A(0,
的图象在点A(0,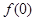 )处的切线方程;
)处的切线方程;
(II)讨论函数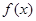 的单调性;
的单调性;
(Ⅲ)是否存在实数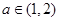 ,使
,使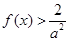 当
当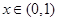 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数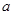 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分12分)设函数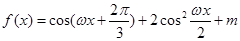 (
(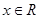 )的最大值为
)的最大值为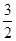 ,且其图象相邻两对称中心之间的距离为
,且其图象相邻两对称中心之间的距离为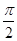 .
.
(Ⅰ)求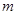 、
、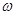 的值;
的值;
(Ⅱ)求 在区间
在区间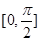 上的最值.
上的最值.
(本小题满分16分)已知数列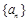 满足
满足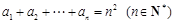 .
.
(1)求数列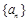 的通项公式;
的通项公式;
(2)对任意给定的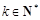 ,是否存在
,是否存在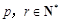 (
( )使
)使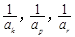 成等差数列?若存在,用
成等差数列?若存在,用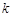 分别表示
分别表示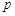 和
和 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为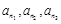 .
.
(本小题满分16分)已知函数 的图象上,以N(1,n)为切点的切线的倾斜角为
的图象上,以N(1,n)为切点的切线的倾斜角为 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式 ≤k-1991对于
≤k-1991对于 恒成立;
恒成立;
(3)求证: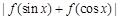 ≤
≤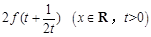 .
.
(本小题满分14分)直棱柱 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,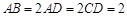 .
.
(1)求证:AC⊥平面BB1C1C;
(2)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
(本小题满分14分)在平面直角坐标系 中,不共线的四点
中,不共线的四点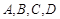 满足
满足 且
且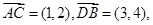
(1)求向量 的坐标;
的坐标;
(2)求四边形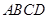 的面积.
的面积.