(本小题12分)已知数列 有
有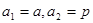 (常数
(常数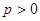 ),对任意的正整数
),对任意的正整数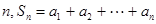 ,并有
,并有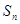 满足
满足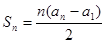 。
。
(Ⅰ)求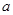 的值并证明数列
的值并证明数列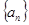 为等差数列;
为等差数列;
(Ⅱ)令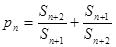 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式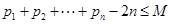 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。
如图,在直三棱柱ABC-A1B1C1中, E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角A1-AG-E的大小(文科求其正切值)。
矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD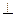 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD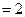 , AD=1, EF=
, AD=1, EF=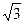 .
.
(Ⅰ)证明:AE 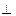 平面FCB;
平面FCB;
(Ⅱ)求异面直线BD与AE所成角的余弦值
(Ⅲ)若M是棱AB的中点,在线段FD上是否存在一点N,使得MN∥平面FCB?
证明你的结论.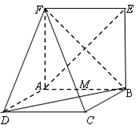
在五棱锥P-ABCDE中,PA=AB=AE=4a,PB=PE= a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若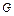 为
为 中点,求证:
中点,求证: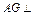 平面
平面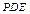 .
.
(2)求二面角A-PD-E的正弦值;(3)求点C到平面PDE的距离.
如图,在几何体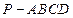 中,面
中,面 为矩形,
为矩形,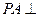 面
面 ,
,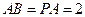
(1)求证;当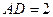 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;
(2)当 时,求二面角
时,求二面角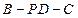 的取值范围。
的取值范围。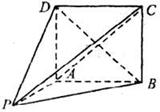
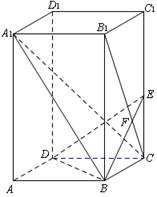
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
(1)求证:A1C⊥平面BDE;
(2)求A1B与平面BDE所成角的正弦值。
(3)设F是CC1上的动点(不包括端点C),求证:△DBF是锐角三角形。