如图,在等腰梯形ABCD中,AB‖CD,已知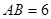 ,
,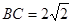 ,
,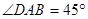 ,以
,以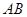 所在直线为
所在直线为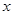 轴,
轴,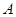 为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转
为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转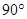 得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图).
得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图). 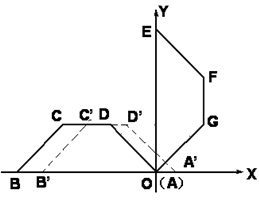
⑴在直线DC上是否存在一点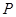 ,使
,使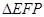 为等腰三角形,若存在,写出出
为等腰三角形,若存在,写出出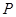 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
⑵将等腰梯形ABCD沿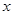 轴的正半轴平行移动,设移动后的
轴的正半轴平行移动,设移动后的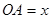 (0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为
(0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为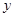 ,求
,求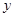 与
与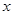 之间的函数关系式.并求出重叠部分的面积的最大值。
之间的函数关系式.并求出重叠部分的面积的最大值。
如图是建有平面直角坐标系的正方形网格,请按下列要求操作: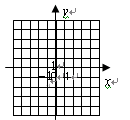
(1)画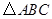 ,使
,使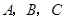 三点的坐标分别为
三点的坐标分别为 ;
;
(2)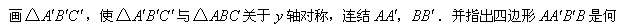 种特殊的四边形?
种特殊的四边形?
(1)解不等式: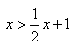 ;
;
(2).计算: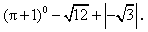
在 中,
中, 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设 的面积为
的面积为 ,求
,求 与月份
与月份 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)当 为何值时,
为何值时, 为直角三角形。
为直角三角形。
为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:
| 月份 销售额 |
销售额(单位:元) |
|||||
| 1月 |
2月 |
3月 |
4月 |
5月 |
6月 |
|
| 小李(A公司) |
11600 |
12800 |
14000 |
15200 |
16400 |
17600 |
| 小张(B公司 |
7400 |
9200 |
1100 |
12800 |
14600 |
16400 |
(1)请问小李与小张3月份的工资各是多少?
(2)小李1~6月份的销售额 与月份
与月份 的函数关系式是
的函数关系式是 小张1~6月份的销售额
小张1~6月份的销售额 也是月份
也是月份 的一次函数,请求出
的一次函数,请求出 与
与 的函数关系式;
的函数关系式;
(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。
如图,点P在 的直径BA的延长线上,AB=2PA,PC切
的直径BA的延长线上,AB=2PA,PC切 于点C,连结BC。
于点C,连结BC。
(1)求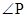 的正弦值;
的正弦值;
(2)若 的半径r=2cm,求BC的长度。
的半径r=2cm,求BC的长度。