某学习小组在探索各内角都相等的圆内接多边形是否为正多边形时，-优题课

某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，有如下探讨：
甲同学：我发现这种多边形不一定是正多边形．如圆内接矩形不一定是正方形．
乙同学：我知道边数为3时，它是正三角形；我想，边数为5时，它可能也是正五边形…
丙同学：我发现边数为6时，它也不一定是正六边形．如图2，△ABC是正三角形，弧AD、弧BE、弧CF均相等，这样构造的六边形ADBECF不是正六边形．

（1）如图1，若圆内接五边形ABCDE的各内角均相等，则∠ABC= °，并简要说明圆内接五边形ABCDE为正五边形的理由；
（2）如图2，请证明丙同学构造的六边形各内角相等；
（3）根据以上探索过程，就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n（n≥3，n为整数）”的关系，提出你的猜想（不需证明）．

科目数学题型解答题难度较难

知识点：圆幂定理

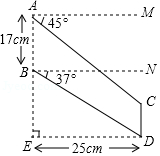
“ $C 919$ ”大型客机首飞成功，激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中 $AB / / CD$ ， $AM / / BN / / ED$ ， $AE ⊥ DE$ ，请根据图中数据，求出线段 $BE$ 和 $CD$ 的长． $(\sin 37 ° \approx 0.60$ ， $\cos 37 ° \approx 0.80$ ， $\tan 37 ° \approx 0.75$ ，结果保留小数点后一位）

如图，在网格中，每个小正方形的边长均为1个单位长度，我们将小正方形的顶点叫做格点，线段 $AB$ 的端点均在格点上．

（1）将线段 $AB$ 向右平移3个单位长度，得到线段 $A' B'$ ，画出平移后的线段并连接 $AB'$ 和 $A' B$ ，两线段相交于点 $O$ ；

（2）求证： $ΔAOB ≅$ △ $B' OA'$ ．

某校为了解学生的每周平均课外阅读时间，在本校随机抽取若干名学生进行调查，并将调查结果绘制成如下不完整的统计图表，请根据图表中所给的信息，解答下列问题：

组别	阅读时间 $t$ （单位：小时）	频数（人数）
$A$	$0 ⩽ t < 1$	8
$B$	$1 ⩽ t < 2$	20
$C$	$2 ⩽ t < 3$	24
$D$	$3 ⩽ t < 4$	$m$
$E$	$4 ⩽ t < 5$	8
$F$	$t ⩾ 5$	4

（1）图表中的 $m =$ 　　， $n =$ 　　；

（2）扇形统计图中 $F$ 组所对应的圆心角为　　度；

（3）该校共有学生1500名，请估计该校有多少名学生的每周平均课外阅读时间不低于3小时？

已知，在 $Rt Δ ABC$ 中， $∠ ACB = 90 °$ ， $AC = 4$ ， $BC = 2$ ， $D$ 是 $AC$ 边上的一个动点，将 $ΔABD$ 沿 $BD$ 所在直线折叠，使点 $A$ 落在点 $P$ 处．

（1）如图1，若点 $D$ 是 $AC$ 中点，连接 $PC$ ．

①写出 $BP$ ， $BD$ 的长；

②求证：四边形 $BCPD$ 是平行四边形．

（2）如图2，若 $BD = AD$ ，过点 $P$ 作 $PH ⊥ BC$ 交 $BC$ 的延长线于点 $H$ ，求 $PH$ 的长．

如图，抛物线 $y = a (x - 1) (x - 3)$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴的正半轴交于点 $C$ ，其顶点为 $D$ ．

（1）写出 $C$ ， $D$ 两点的坐标（用含 $a$ 的式子表示）；

（2）设 $S_{ΔBCD} : S_{ΔABD} = k$ ，求 $k$ 的值；

（3）当 $ΔBCD$ 是直角三角形时，求对应抛物线的解析式．