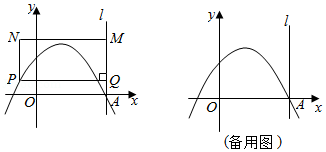
如图,在平面直角坐标系中,抛物线 与 轴正半轴交于点 ,且点 的坐标为 ,过点 作垂直于 轴的直线 . 是该抛物线上的任意一点,其横坐标为 ,过点 作 于点 , 是直线 上的一点,其纵坐标为 .以 , 为边作矩形 .
(1)求 的值.
(2)当点 与点 重合时,求 的值.
(3)当矩形 是正方形,且抛物线的顶点在该正方形内部时,求 的值.
(4)当抛物线在矩形 内的部分所对应的函数值 随 的增大而减小时,直接写出 的取值范围.
如图所示,电工李师傅借助梯子安装天花板上距地面2.90m的顶灯,已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m,矩形面与地面所成的角α为78°,李师傅的身高为1.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便。
(1)为了安全在梯子的第二段间接一根绳子,绳子最短应是多少?(两边打结处共用绳0.6m)
(2)他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他 安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
①试探究AE与⊙O的位置关系,并说明理由;
②已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O的半径r的一种方案;
1) 你选用的已知数是_________;
2) 写出求解过程(结果用字母表示).
据研究,当洗衣机中洗衣粉的含量在0.2%~0.5%之间时,衣服的洗涤效果较好,因为这时表面活性较大,现将4.94千克的衣服放入最大容量为15kg的洗衣机中,欲使洗衣机中洗衣粉的含量达到0.4%,那么洗衣机中需要加入多少千克水,多少匙洗衣粉?(1匙洗衣粉约0.02kg,假设洗衣机以最大容量洗涤)
某班同学对南昌市市民对于“八一南昌起义”这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”“不知道”四级将调查结果绘制成以下统计表和条形统计图

(1)这次调查的样本容量是
(2)若将四种情况用扇形统计图表示,则“了解”和“知道”两种情况所对圆心角和为
度
(3)补充统计表和条形统计图
(4)若南昌市共有市民480万人,请你估计“清楚”这一事件的可能有多少人?
有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2。B布袋中有三个完全相同的小球,分别标有数字—1,—2和—3。小明从A布袋中随机抽出一个小球,记录其标有的数字为 ,再从B布袋中随机抽出一个小球,记录其标有的数字为
,再从B布袋中随机抽出一个小球,记录其标有的数字为 。他用这两个数字确定一个点P的坐标为
。他用这两个数字确定一个点P的坐标为
(1)用 列表或画树状图的方法点P的所有可能坐标
列表或画树状图的方法点P的所有可能坐标
(2)求点P落在直线 上的概率
上的概率