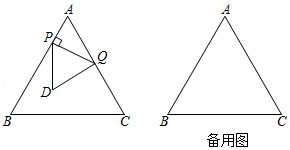
如图, 是等边三角形, ,动点 从点 出发,以 的速度沿 向点 匀速运动,过点 作 ,交折线 于点 ,以 为边作等边三角形 ,使点 , 在 异侧.设点 的运动时间为 , 与 重叠部分图形的面积为 .
(1) 的长为 (用含 的代数式表示).
(2)当点 落在边 上时,求 的值.
(3)求 关于 的函数解析式,并写出自变量 的取值范围.
问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.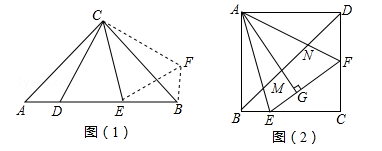
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2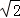 ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是 (只填写序号).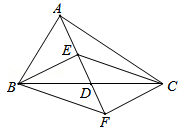
(·辽宁锦州)如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
(·辽宁本溪)如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与 围成的阴影部分的面积S.
围成的阴影部分的面积S.
如图①,半径为R,圆心角为n°的扇形面积是 ,由弧长l=
,由弧长l= ,得
,得 =
= •
• •R=
•R= lR.通过观察,我们发现S扇形=
lR.通过观察,我们发现S扇形= lR类似于S三角形=
lR类似于S三角形= ×底×高.
×底×高.
类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.
(1)设扇环的面积为S扇环, 的长为
的长为 ,
, 的长为
的长为 ,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=
,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形= ×(上底+下底)×高,用含
×(上底+下底)×高,用含 ,
, ,h的代数式表示S扇环,并证明;
,h的代数式表示S扇环,并证明;
(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?