在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
58 |
96 |
116 |
295 |
484 |
601 |
摸到白球的频率 |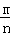
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |
（1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）
（2）试估算口袋中白种颜色的球有多少只？
（3）请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？
（Ⅰ）化简：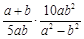
；
（Ⅱ）解分式方程：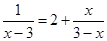
数与数之间的关系真奇妙，例如：①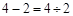
；②
；③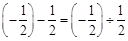
．某教师分析如下：⑴以上这些等式都有一个共同特征：两个实数的差等于这两个实数的商；⑵如果等号左边的第一个实数用
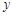表示，第二个实数用
表示，则可以得到一个关于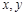
的关系式．请你根据以上分析，再找出一组满足上述特征的两个实数，并写成等式形式：．
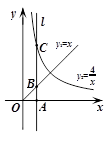
如图所示，过点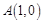
作垂直
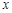轴的直线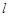
，分别交函数
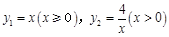图象于
两点，则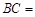
．
如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t(秒)．
（1）当t为何值时，四边形PQDC是平行四边形．
（2）当t为何值时，以C，D，Q，P为顶点的梯形面积等于60cm2？
（3）是否存在点P，使△PQD是等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由．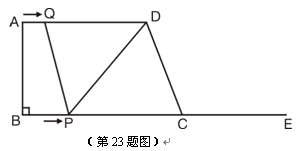
如图，已知四边形ABCD是边长为2的正方形，以对角线BD为边作正三角形BDE，过E作DA 的延长线的垂线EF，垂足为F。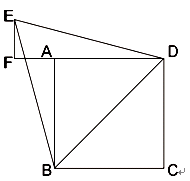
（1）找出图中与EF相等的线段，并证明你的结论；
（2）求AF的长。