如图,在平行四边形ABCD中,AD="4" cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2.
① 求S关于t的函数关系式;
② 求S的最大值.
如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.
如图,D是AB上一点,DF交AC于点E,AE=EC,CF∥AB.求证:AD=CF.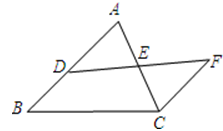
如图所示,点B,E,C,F在同一直线上,AB=DE,∠B=∠DEF,BE=CF.求证:AC=DF.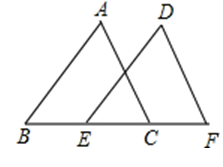
某种上屏每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图像如图所示.
销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
销售单价在什么范围时,该种商品每天的销售利润不低于16元?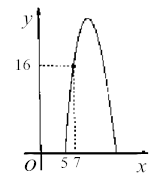
几个小伙伴打算去音乐厅观看演出,他们准备用360元购买门票.下面是两个小伙伴的对话:
根据对话的内容,请你求出小伙伴们的人数.