先化简,再选一个合适的数代入求值: .
解不等式组 .
计算: .
已知函数 , 均为一次函数, 为常数.

(1)如图1,将直线 绕点 逆时针旋转 得到直线 ,直线 交 轴于点 .若直线 恰好是 , 中某个函数的图象,请直接写出点 坐标以及 可能的值;
(2)若存在实数 ,使得 成立,求函数 , 图象间的距离;
(3)当 时,函数 图象分别交 轴, 轴于 , 两点, 图象交 轴于 点,将函数 的图象最低点 向上平移 个单位后刚好落在一次函数 图象上.设 的图象,线段 ,线段 围成的图形面积为 ,试利用初中知识,探究 的一个近似取值范围.(要求:说出一种得到 的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.
菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .
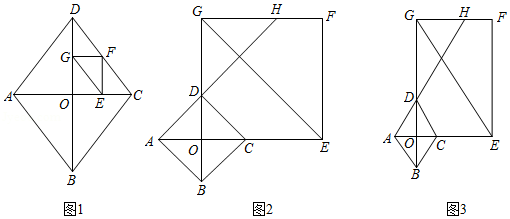
(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.