菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .
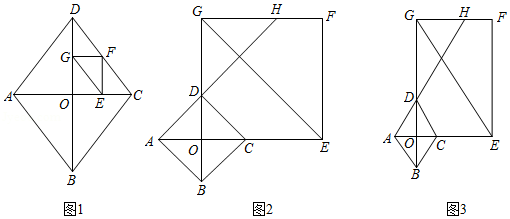
(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.
解方程: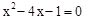
已知直线 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.
(1)当点C坐标为(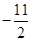 ,
, )时,求直线AB的解析式;
)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数 的图像上,求点D到直线AB的距离;
的图像上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数 有最小值-3,求实数m的值.
有最小值-3,求实数m的值.
如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.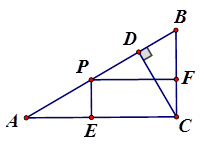
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
东方商场购进一批单价为20元的日用品,销售一段时间后,经调查发现,若按每件24元的价格销售时,每月能卖36件;若按每件29元的价格销售时,每月能卖21件,假定每月销售件数y(件)与价格x(元/件)之间满足关系一次函数.
(1)试求y与x的函数关系式;
(2)为了使每月获得利润为144元,问商品应定为每件多少元?
(3)为了获得了最大的利润,商品应定为每件多少元?
如图,AB是⊙O的直径,点C在⊙O上,D是AB延长线上的一点,AE⊥DC交DC的延长线于E,AC平分∠DAE.
(1)直线DE与⊙O有怎样的位置关系?为什么?
(2)若AC= ,⊙O的半径为1,求CD的长及由弧BC、线段BD、CD所围成的阴影部分的面积.
,⊙O的半径为1,求CD的长及由弧BC、线段BD、CD所围成的阴影部分的面积.