如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.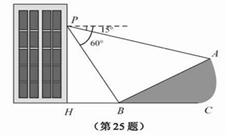
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ≈1.732).
≈1.732).
数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如
下: 
小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元
的小家电.通过试营销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)
与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设王强每月获得的利润为p(元),求p与x之间的函数关系式;如果王强想要每月获得2400元的
利润,那么销售单价应定为多少元?
今年5月31日是世界卫生组织发起的第25个“世界无烟日”.为了更好地宣传吸烟的危害,某中学八年级一班数学兴趣小组设计了如下调查问卷,在达城中心广场随机调查了部分吸烟人群,并将调查结果绘制成统计图. 

根据以上信息,解答下列问题:
(1)本次接受调查的总人数是人,并把条形统计图补充完整.
(2)在扇形统计图中,C选项的人数百分比是,E选项所在扇形的圆心角的度数是.
(3)若通川区约有烟民14万人,试估计对吸烟有害持“无所谓”态度的约有多少人?你对这部分人群有何建议?
如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=900,抛物线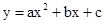 经过A、B、C三点,其顶点为M.
经过A、B、C三点,其顶点为M.
求抛物线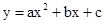 的解析式;
的解析式;
试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
在抛物线上是否存在点N,使得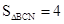 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。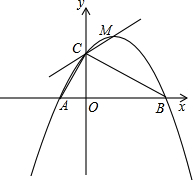
如果方程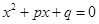 的两个根是
的两个根是 ,那么
,那么 请根据以上结论,解决下列问题:
请根据以上结论,解决下列问题:
已知关于 的方程
的方程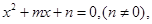 求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
已知 满足
满足 ,求
,求 ;
;
已知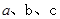 满足
满足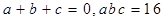 求正数
求正数 的最小值。
的最小值。